
Why are mathematical models and representations important?
Mathematics is deeply abstract. Some people, such as theoretical physicists, computer programmers, data scientists, cryptographers, or engineers, find this fascinating and appreciate the incontestable truths of mathematics that can be used to solve a wide range of problems. But for others, the abstract nature of mathematics can be challenging.
Mathematical models, or representations, are critical tools for helping those who find the abstract nature of mathematics challenging see and understand math concepts (NRC, 2001). High-quality instructional materials must include a varied and aligned use of models to support student learning.
The strategic use of models during instruction has a demonstrated impact on student learning. According to Hattie et al. (2017), using models and representations during mathematics instruction has an effect size of 0.50, a moderate effect that falls within the zone of desired effects. This means that when mathematical representations are used appropriately, student learning exceeds what’s expected in a typical school year.
This research is one reason the National Council of Teachers of Mathematics (NCTM) included using and connecting mathematical representations as one of eight research-informed instructional strategies in Principles to Actions: Ensuring Mathematical Success for All. According to the authors, “Effective teaching of mathematics engages students in making connections among mathematical representations to deepen understanding of mathematics concepts and procedures and as tools for problem solving” (NCTM, 2014/2024).
Into Math’s approach to mathematical models
High-quality math curricula that integrate mathematical representations are essential to student success. Consistent with the research, Into Math—in both its print and digital formats—aligns specific models with the math concepts to be learned and the cognitive level of the learning task (Hattie, 2023).
It is an intentional approach that does not focus on a single model or even just a few. Instead, the program includes a wide variety of representations across grade levels, allowing teachers to leverage the one that best aligns with the mathematical concept and task to maximize student learning. Into Math also includes multiple types of models: physical (manipulatives), visual, symbolic, verbal, and contextual representations (NCTM, 2014/2024). The instructional emphasis is on connecting different representations to deepen understanding, improve engagement, and provide students with tools to communicate their mathematical ideas.
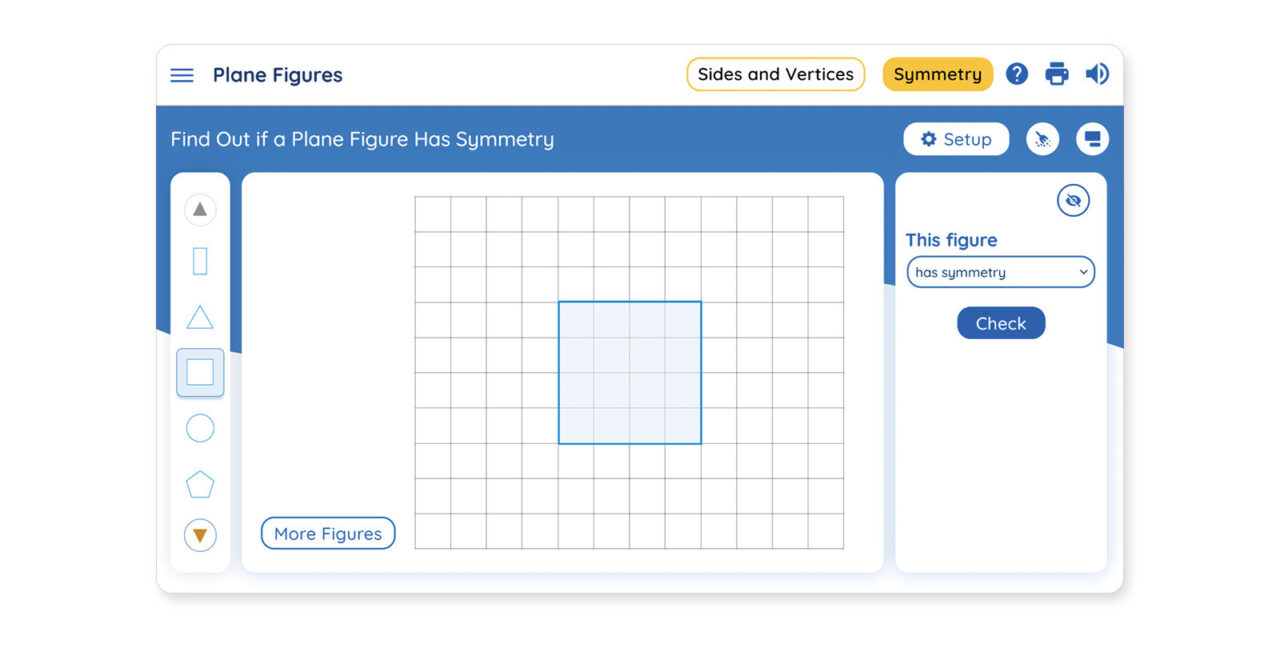
The example above from Into Math Grade 4 shows one representation of plane figures that students see and can interact with.
Additionally, using varied representations gives students different “lenses” through which to access the mathematics. For example, Into Math provides comprehensive support for multilingual learners and students of other special populations. Multiple representations also allow more students to participate in mathematical discourse through features like “Turn and Talk,” which deepens their understanding and ability to communicate their thinking (Tripathi 2008; Fuson & Murata, 2007). Into Math leverages a wide range of math models across all grade levels, as summarized in the table below.
Major mathematical models and representations in Into Math
| Grade level | Models/representations |
| Kindergarten | Pattern blocks, number tiles, two-color counters, color tiles, linking cubes, and drawings |
| Grade 1 | Base-ten blocks, pattern blocks, two-color counters, number cubes, linking cubes, ten frame, number line, and drawings |
| Grade 2 | Base-ten blocks, color tiles, two-color counters, pattern blocks, number cubes, drawings/quick drawings, linking cubes, number line, bar model, ten frame, place value chart, hundred chart, and arrays |
| Grade 3 | Base-ten blocks, color tiles, two-color counters, pattern blocks, fraction tiles, fraction circles, linking cubes, drawing/quick drawings, place value chart, number line, hundred chart, open number line, bar model, and arrays |
| Grade 4 | Base-ten blocks, color tiles, pattern blocks, two-color counters, fraction tiles, fraction circles, fraction strips, linking cubes, place value chart, number line, bar model, drawings/quick drawings, open number line, arrays, and area model |
| Grade 5 | Base-ten blocks, pattern blocks, two-color counters, fraction tiles, fraction circles, fraction strips, place value chart, color tiles, number line, arrays, drawings/quick drawings, area model, and bar model |
| Grade 6 | Base-ten blocks, algebra tiles, two-color counters, number cubes, fraction tiles, fraction strips, drawings/quick drawings, number line, and drawings |
| Grade 7 | Base-ten blocks, algebra tiles, two-color counters, number cubes, fraction tiles, fraction strips, number line, and drawings |
| Grade 8 | Base-ten blocks, algebra tiles, two-color counters, number cubes, fraction tiles, number line, and drawings |
| Algebra | Algebra tiles, two-color counters, number cubes, verbal model, and drawings |
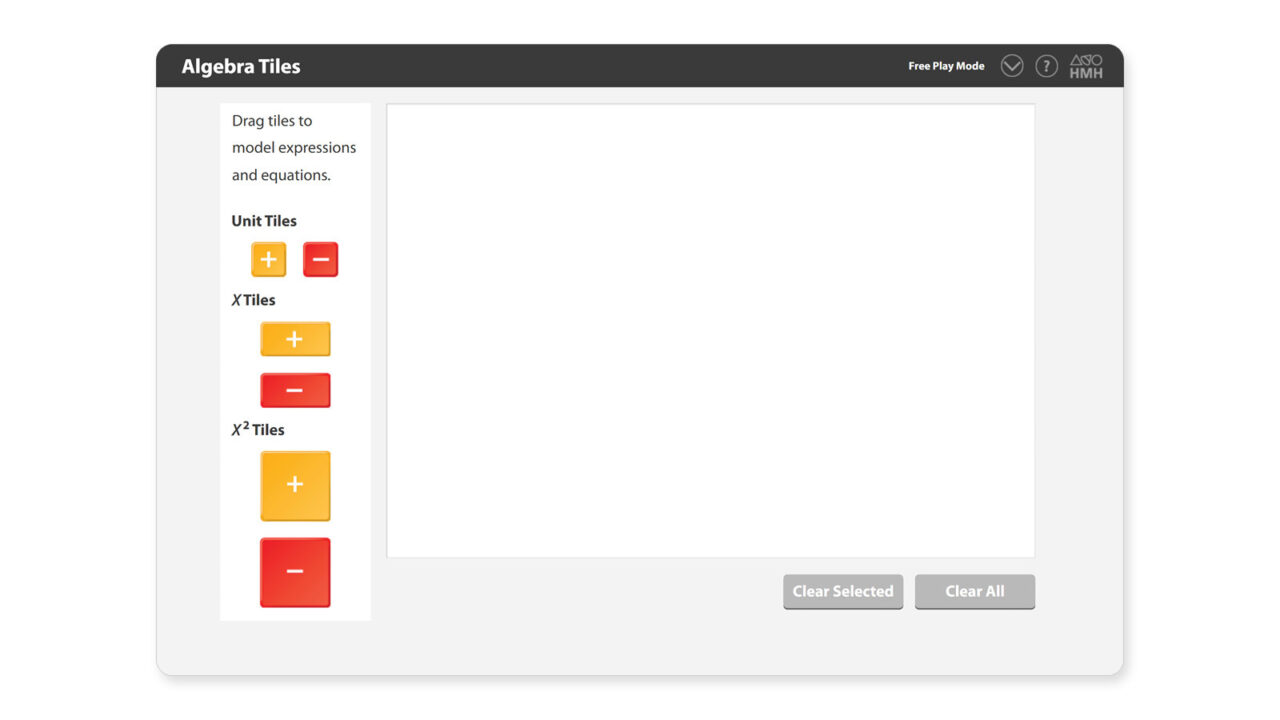
In Into Math, one way that students can model quadratic equations is with algebra tiles.
Implementation of math models in Into Math
In Into Math, math models are never directly taught for the sake of learning the model. Rather, the models represent a mathematical concept or help to reach the lesson’s objective. The representations are simply tools students use to deepen their understanding and solve problems. When models are taught directly instead of being meaningfully used as representations of important mathematical concepts, students may come to see the representation as the goal of learning rather than the mathematics itself (NCTM, 2014/2024).
Making connections leads to a deeper understanding of mathematics. Therefore, consistent with the research, Into Math emphasizes not only various mathematical representations but also, more significantly, how these representations are related (Hattie et al., 2017). Consider the example of learning multiplication of 1- and 2-digit numbers in fourth grade Into Math. Over a series of lessons, students develop an understanding of the standard algorithm by starting with base-ten blocks. The instructional approach then transitions students to the area model, drawings, and finally connects this conceptual understanding to the standard algorithm. This progression allows students to move from a physical model (base-ten blocks) to a visual representation (area model and drawings) before working with the symbolic representation of the partial products (algorithm). This sequence follows the well-established, research-based instructional progression of concrete models to visual representations to symbolic representations (Hattie, 2023).
Teachers support students through this transition by engaging them in discourse focused on the language of place value and multiplication. The “Spark Discussions,” “Turn and Talk,” and “Depth of Knowledge Leveled Questions” features in the Into Math teacher’s edition provide teachers with the purposeful questions needed to ensure students engage in meaningful mathematical discourse (NCTM, 2014/2024).
These instructional features increase the likelihood that students make the necessary connections among representations and develop a deep understanding of the standard multiplication algorithm. This focus on leveled questioning, discourse, and use of drawings and other representations also encourages students to explain their thinking and focuses their attention on the structural features of mathematics, as recommended in the literature on effective instructional strategies (NCTM, 2014/2024).
Effective use of models and representations
Every mathematics program includes mathematical models—it’s impossible to teach math without them. What differentiates mathematics programs and determines whether representations affect student learning is how they are instructionally implemented.
Informed by research on the effective use of models, Into Math implements mathematical representations with an intentional plan to maximize every student’s learning. Into Math uses a wide variety of mathematical representations—from linking cubes in kindergarten to algebra tiles in algebra—to ensure they align with specific learning objectives.
But Into Math goes beyond the inclusion and alignment of mathematical models. Into Math emphasizes students making connections among representations through meaningful mathematical discourse and student drawings. In Into Math, models are not the goal but the vehicle by which every student develops a deep understanding of mathematics and experiences the confidence necessary to become a lifelong learner and user of mathematics.
The views expressed in this article are those of the author and do not necessarily represent those of HMH.
***
Grow student confidence in mathematics with HMH Into Math, our core math solution for Grades K–Algebra 1.
Explore mathematical models in Into Math
- Kindergarten: Counters
- Grade 1: Cubes and drawings
- Grade 2: Place value chart
- Grade 3: Arrays and drawings
- Grade 4: Fraction strips and drawings
- Grade 8: Drawings
- Grade 8: Drawings
References
Fuson, K.C., & Murata, A. (2007). Integrating NRC principles and the NCTM process standards to form a class learning path model that individualizes withing whole-class activities. National Council of Supervisors of Mathematics Journal of Mathematics Education Leadership, 10(1), 72–91.
Hattie, J. (2023). Visible learning: The sequel. Thousand Oaks, CA: Corwin.
Hattie, J. Fisher, D., Frey, N., Gojak, L.M., Moore, S.D., & Mellman, W. (2017). Visible learning for mathematics: What works best to optimize student learning. Thousand Oaks, CA: Corwin.
National Council of Teachers of Mathematics (NCTM). (2014/2024). Principles to Actions: Ensuring mathematical success for all. Reston, VA: Author.
National Research Council (NRC). (2001). Adding it up: Helping children learn mathematics. Washington, D.C.: National Academies Press.
Tripathi, P.N. (2008). Developing mathematical understanding through multiple representations. Mathematics Teaching in the Middle School, 13(8), 438–445.
Get our FREE guide “Optimizing the Math Classroom: 6 Best Practices.”












